Возрастное ограничение 18+
Екатеринбуржцы жалуются на неисполненное обещание по очистке улиц врио мэра Орлова

Исполняющий обязанности главы Екатеринбурга Алексей Орлов заявил вчера, что дороги столицы Урала будут очищены от снега к утру понедельника. Однако этого не случилось и к обеду, считают пользователи соцсетей.
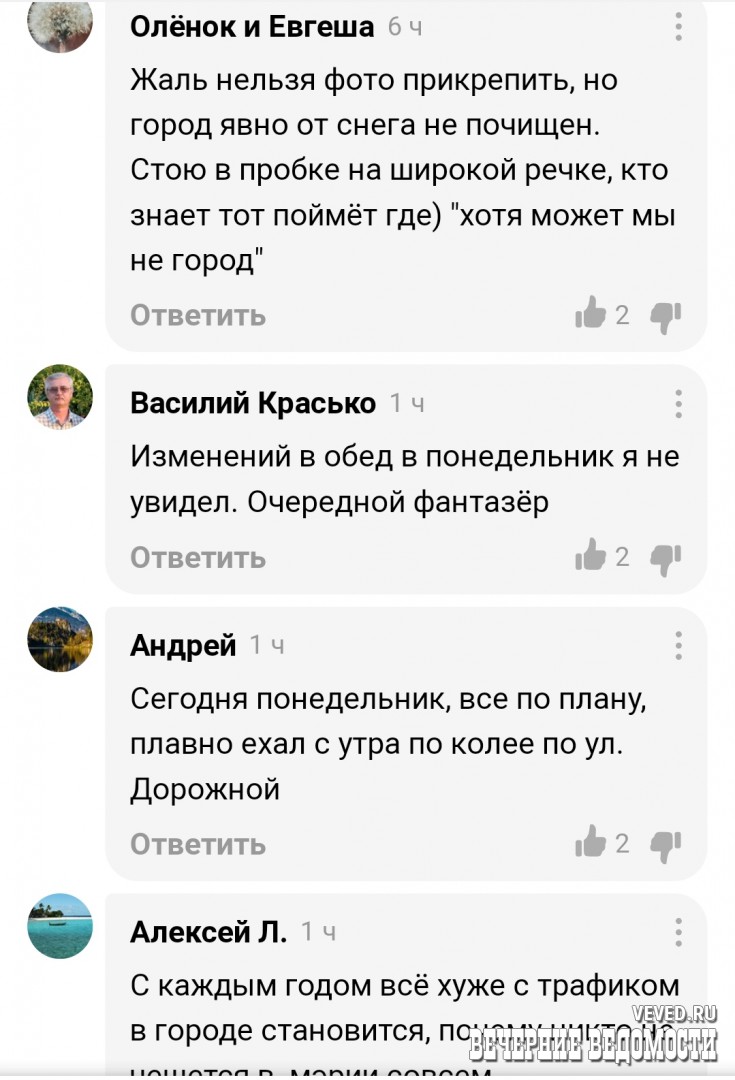
«Изменений в обед в понедельник я не увидел. Очередной фантазёр», – пишет пользователь Василий Краско в комментариях под новостью в Яндексе.
А в Фейсбуке предположили, что предыдущий мэр Екатеринбурга забрал с собой всю снегоуборочную технику.
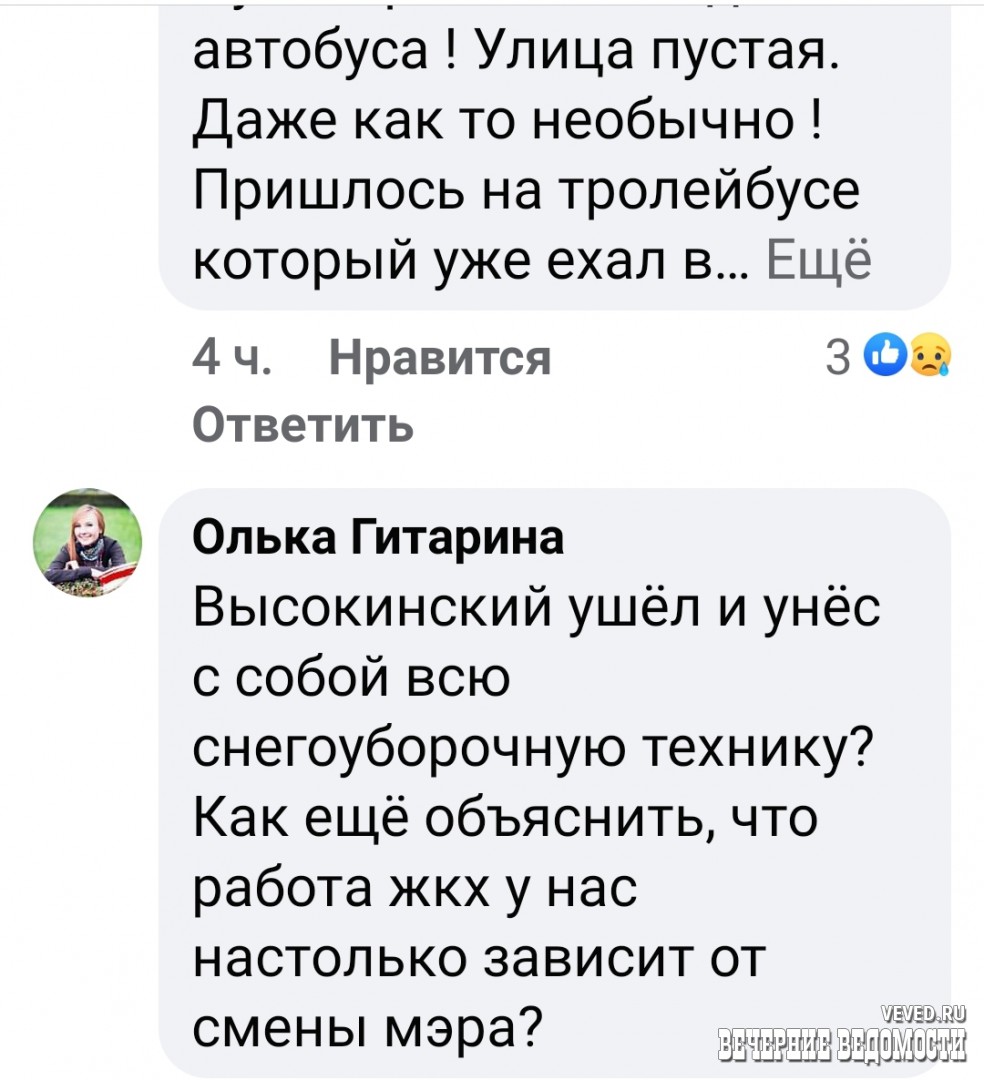
«Высокинский ушёл и унёс с собой всю снегоуборочную технику? Как ещё объяснить, что работа жкх у нас настолько зависит от смены мэра?», – написала в комментариях под новостью «Вечерних ведомостей» об обещании Орлова пользователь Олька Гитарина.
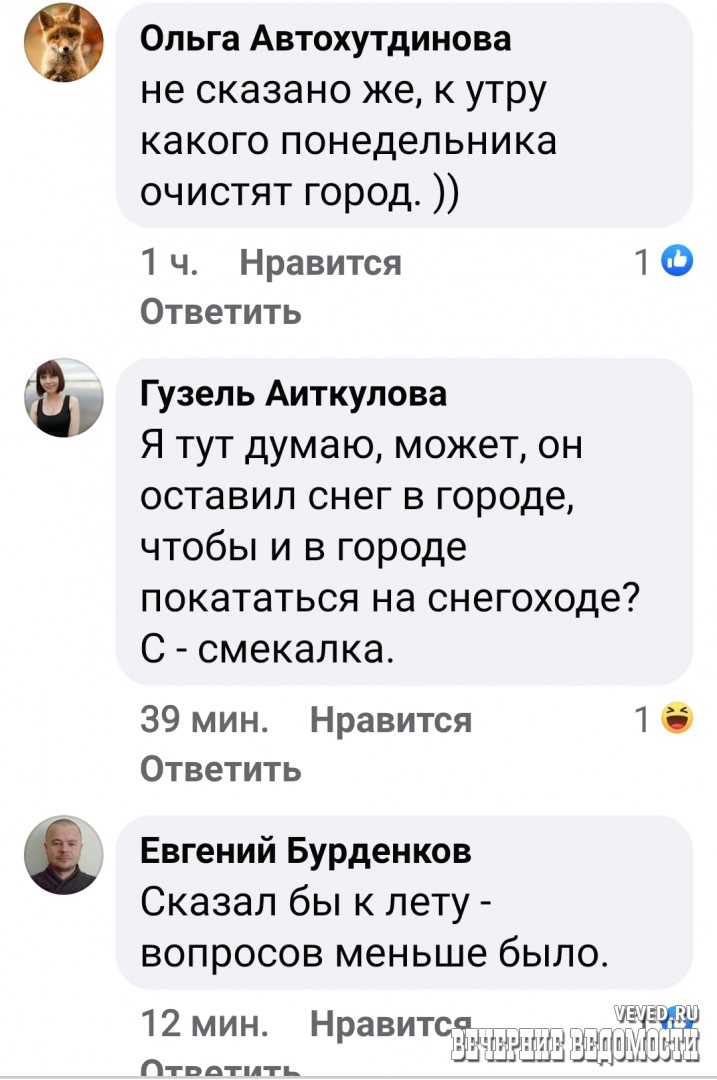
Другие пользователи считают, что Орлов же не сказал, к какому понедельнику почистит – значит, очевидно, не к сегодняшнему.
«Сказал бы к лету - вопросов меньше было», – заметил Евгений Бурденков.
Также в комментариях предположили, что Орлов не проконтролировал, несмотря на свое обещание, очистку улиц от снега, чтобы «и в городе покататься на снегоходе».
Напомним, пока Екатеринбург утопал в снеге, автомобилисты жаловались на заваленные дороги, исполняющий обязанности мэра Екатеринбурга Алексей Орлов выложил фотографию в своем Инстаграм, на которой он катается на снегоходе. Фотография возмутила горожан. Орлов, комментируя это фото порталу E1 пообещал, что екатеринбургские дороги будут очищены от снега к утру понедельника.
«Изменений в обед в понедельник я не увидел. Очередной фантазёр», – пишет пользователь Василий Краско в комментариях под новостью в Яндексе.
А в Фейсбуке предположили, что предыдущий мэр Екатеринбурга забрал с собой всю снегоуборочную технику.
«Высокинский ушёл и унёс с собой всю снегоуборочную технику? Как ещё объяснить, что работа жкх у нас настолько зависит от смены мэра?», – написала в комментариях под новостью «Вечерних ведомостей» об обещании Орлова пользователь Олька Гитарина.
Другие пользователи считают, что Орлов же не сказал, к какому понедельнику почистит – значит, очевидно, не к сегодняшнему.
«Сказал бы к лету - вопросов меньше было», – заметил Евгений Бурденков.
Также в комментариях предположили, что Орлов не проконтролировал, несмотря на свое обещание, очистку улиц от снега, чтобы «и в городе покататься на снегоходе».
Напомним, пока Екатеринбург утопал в снеге, автомобилисты жаловались на заваленные дороги, исполняющий обязанности мэра Екатеринбурга Алексей Орлов выложил фотографию в своем Инстаграм, на которой он катается на снегоходе. Фотография возмутила горожан. Орлов, комментируя это фото порталу E1 пообещал, что екатеринбургские дороги будут очищены от снега к утру понедельника.
Получать доступ к эксклюзивным и не только новостям Вечерних ведомостей быстрее можно, подписавшись на нас в сервисах «Яндекс.Новости» и «Google Новости».
Поддержать редакцию


Информация
Комментировать статьи на сайте возможно только в течении 60 дней со дня публикации.







 Осуждённую по статье о госизмене екатеринбурженку с гражданством США могут готовить к обмену
Осуждённую по статье о госизмене екатеринбурженку с гражданством США могут готовить к обмену
 Краснокнижные растения из Берёзовой рощи и Малой Здохни выкопали ради застройки этих объектов
Краснокнижные растения из Берёзовой рощи и Малой Здохни выкопали ради застройки этих объектов
 Согласование стройки мусорного полигона в Сысертском районе выходит на финишную прямую
Согласование стройки мусорного полигона в Сысертском районе выходит на финишную прямую